Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği , ANTRAK tarafından yayınlanan "AMATÖR TELSİZCİLİK  SINAV KILAVUZU ve BAŞVURU KİTABI" içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız

106) İki tane direnç seri bağlandığında eşdeğer direnç 10 ohm, paralel bağlandığında 2,4 ohm'dur. Bu dirençlerin değerleri aşağıdakilerden hangisidir?

a) 5 ve 5 ohm     b) 2 ve 8 ohm

c) 3 ve 7 ohm     d) 4 ve 6 ohm

Çözüm: Bu sorunun cevabı, matematiğin iki bilinmeyenli denklem çözümü v.b. araçlarla yapılabilir. Ama bizim amacımız, olabildiğince kolay yöntemler kullanmaktır.

Seri bağlı iki direncin eşdeğer direnci, dirençlerin değerlerinin toplamına eşittir.

Cevaplara baktığımızda, tüm şıklarda da dirençlerin toplamının 10 Ω olduğunu görmekteyiz. O halde ikinci bakacağımız şey, bu değerlerdeki iki direncin paralel bağlanması durumunda değerinin 2,4 Ω olup olmadığıdır.

Paralel bağlı iki direncin eşdeğer direcini veren formül, aşağıda verilmiştir.

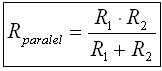
 Bu förmül, iki direncin değerlerinin çarpımının, dirençlerin toplamına bölüneceğini gösteriyor. Şimdi tek tek her şıktaki değerleri tablo halinde bu formüle uygulayalım:

Doğru cevap "d" seçeneğidir.

107) Şekildeki devrede r ve R bilinmeyen dirençlerdir. A ampermetresinin sıfır göstermesi için R'nin değeri ne olmalıdır?

             a) 3 ohm           b) 32 ohm        c) 6 ohm           d) 2,5 ohm

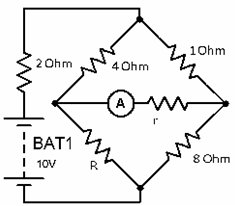
 Çözüm: Devre, bir "Wheatstone" köprüsüdür. Kare şeklindeki köprünün ana kolları, R direnci; 4 Ω ; 1 Ω ve 8 Ω dirençleridir. Ampermetre ve ona seri bağlı direnç ölçüm içindir. Devrenin yan tarafındaki 10 voltluk batarya ve ona seri bağlı 2 Ω direnç, besleme içindir. Bu tip köprü devreleri, direnç ölçmek amacıyla kullanılır. Değerini bilmediğimiz direnç R direnci olup, köprünün kollarından birini oluşturur. Amacımız, köprünün öbür kollarına değerlerini bildiğimiz dirençler koyarak, ampermetreden sıfır değerini görmektir. Bu durum elde edildiğinde, köprü dengeye geldi demektir. Dengedeki Wheatstone köprüsünde bilmemiz gereken, "birbirine paralel iki kenardaki (geometrik olarak paralellik kastediliyor) dirençlerin değerlerinin çarpımı, öteki paralel iki kenardaki dirençlerin çarpımına eşittir." Yani R direnci ile 1 Ω değerlerinin çarpımı ile 8 Ω ve 4 Ω değerlerinin çarpımı eşit olmalıdır. R x 1 Ω = 8 Ω x 4 Ω =32. Burada dikkat etmemiz gereken konu, dirençlerin birimi olup, yukarıdaki formüllerde hepsini ohm Ω cinsinden kullanmaktır. Bunun sonucunda da bilinmeyen direnç ohm Ω cinsinden bulunur.

R= (4 x 8) / 1 = 32 Ω

Buradan, cevabın "b" seçeneği olduğu anlaşılıyor.

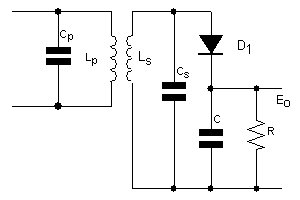
107) Şekilde görülen devrede

    ve

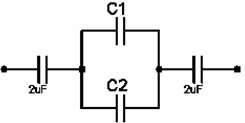
ise C₁ ve C₂ yi  bulunuz.

a) 4 ve 8µF    b) 3 ve 6µF   c) 1 ve 2µF    d) 6 ve 12µF

Çözüm: paralel bağlı iki kondansatör ile bunlara seri bağlı iki kondansatörün eşdeğer kapasitesi 9/10 μF olarak verilmiş. Değerleri bilinen iki kondansatörün, sistemin dış tarafında olmasına rağmen, seri olmaları nedeniyle peşpeşe olduklarını düşünebiliriz. O halde seri bağlı ve değerleri 2 μF olan iki kondansatörün eşdeğer kapasitesini bulabiliriz.

Seri bağlı iki konsatörün eşdeğer kapasitesinin veren formül aşağıdadır.

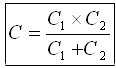
 (107-1)

Buna göre seri bağlı iki adet 2 μF, C=(2×2)/(2+2) formülü uyarınca 1 μF eşdeğer kapasite oluşturur. Şimdi sistemi, paralel C1 ve C2 ile onlara seri bir adet 1 μF'dan oluşuyor diye düşünebiliriz.

Paralel C1 ve C2 kapasitesi bilinmediği için onları Cp sembolü ile gösterelim. Cp ve 1 μF seri olduğu için, eşdeğer kapasite yine (107-1) formülü kullanılarak elde edilir.

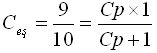
Buradan 9x (Cp+1) = 10 x (Cp X 1)  ->  9Cp + 9 = 10Cp -> Cp = 9 μF bulunur.

Paralel bağlı iki kondansatörün değeri, kapasitelerinin toplamına eşittir.

formülü uyarınca, toplamı 9 μF olan ve soruda

şeklinde oranları verilen kapasite değerleri 3 μF ve 6 μF olur. (Yani oranları bire karşı iki olup, toplamları da 9 eden iki sayı 3 ve 6 dır).

Doğru cevap "b" seçeneğidir.

109)  Şekilde görülen değişken direncin (R) değeri kaça ayarlanmalıdır ki 5 ohm'luk dirençteki güç 20 Watt olsun?

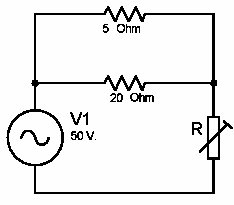
a) 16 ohm          b) 10 ohm         c) 20 ohm           d) 32 ohm

Çözüm: Bir direncin gücü ile, akım ve gerilim arasındaki bağıntı aşağıdaki formülde verilmiştir.

Bu denklemde

denkleminden

 çıkar.     5Ω direncin voltajı 10 volt ise, Ohm kanunu

gereğince akım, I₅ = 10/5= 2 A bulunur. 20Ω ve 5Ω paralel olduğu için, voltajlar (V₂₀=10 V) aynı olur. O halde 20Ω un akımı

kullanılarak I₂₀ = 10/20 = 0.5 A bulunur. Sözedilen iki direncin akımları toplanarak (Kirşof  kanunu) R direncinin üst noktasına girerler, yani I_R = 2 + 0.5 = 2.5 A . R direncinin voltajı ile 20Ω ( ya da 5Ω ) direncin voltajının toplamı giriş voltajı olan 50 V'a eşittir. 50 V = V₂₀ + V_R = 10 + V_R à  V_R = 50 -10 =40 V bulunur. Ohm kanunu

kullanılarak, R = 40 / 2.5 = 16Ω hesaplanır.

Doğru cevap "a" seçeneğidir.

110) Kapasitans biriminin farad olduğu bilinmektedir. 1 Farad aşağıdakilerin hangisi ile eşdeğerdir?

a) 10³ mikrofarad          b) 10⁶ pikofarad        c) 10¹² mikrofarad        d) 10¹² pikofarad

Çözüm: Bu soruyu ancak ezberden bilirseniz cevaplarsınız. Zor olsa da aşağıdaki tabloyu ezberlemek zorundasınız.

Doğru cevap"d" seçeneğidir.

Teknik soruları cevaplamaya gelecek ay da  devam etmek  üzere hoşça kalınız.

Temel Y. METİN

TB2CBB

   Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği, ANTRAK tarafından yayınlanan “Amatör Telsizcilik Sınav Kılavuzu ve Başvuru Kitabı” içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız.

101.  Şekildeki dalga sisteminde A ve B noktaları arasındaki uzaklık 6 metredir. C noktasından dakikada 7800 dalga geçtiğine göre dalganın yayılma hızı nedir?

a) 780 m/s    b) 130 m/s    c) 1300 m/s    d) 468 m/s

Çözüm : Şekilden dalga boyunu 6 m. olarak görüyoruz. Dalga boyu ,  birbirini izleyen iki tepe noktası veya iki dip noktası arasındaki aralıktır. Öte yandan C noktasından dakikada 7800 dalga geçerse, 7800 kez dalga boyu geçiyor demektir. Dalga dakikada 7800 x 6m. = 46800 m. hızla yol alıyor ! Bu demektir ki dalganın hızı 46800 m. / dak. olur. 1 saniyede ise 46800 / 60 = 780 m. yol alır. Yani dalganın hızı 780 m./sn. olur.

Doğru yanıt “a” seçeneğidir.

102.  Bir kondansatörün değeri, yalıtkan maddenin dielektrik sabiti ile hesaplanır. Mikanın dielektrik sabiti 6, kağıdın ise 2 dir. Mika ve kağıt dielektrikli kondansatörler hangi değerler bölgesinde kullanılır?

a) 0.001 – 1 F                        b) 0.001 – 1 µF

c) 0.001 – 1 pF                       d) 0.001 – 1 nF

Çözüm : Bu soru , radyo amatör adaylarının deneyim ve önbilgi düzeylerini sınamak için sorulmuş sorulara örnektir !

Kağıt veya mika yalıtkanlı , normal boyutlardaki bir kondansatörün değerinin 1F veya 1 µF değerlerine erişmesi olanaksızdır. Yani “a” ve “b” seçeneklerini eleriz. Öte yandan 1pF gibi bir değer de çok düşük gelmektedir. Kağıt ve mika için  0.001 – 1 nF değerleri uygundur.

Doğru yanıt “d” seçeneğidir.

103. Şekilde görülen alçak geçirgen RL süzgecinin frekans grafiğinde, yarı güç frekansını bulunuz (p=3 alınız)

a) 60 Hz       b) 50 Hz        c) 20 Hz        d) 10 Hz

Çözüm : Sorudaki frekans grafiğini oluşturan RL alçak geçirgen süzgeçin şeması yanda görülmektedir. Bu tip filtreler genellikle lambalı devrelerde DC besleme akımındaki dalgayı azaltmak (süzmek) amacıyla doğrultmaç katından sonra kullanılır. Devrede 1200 Ohm olarak verilen direnç, lambalı devrenin toplam sarfiyatını temsil eden ortalama bir değerdir ve gerçek süzgeç çıkışına bu direnç yerine lamba devreleri bağlanır.

Bu süzgeçlerde yarı güç frekansı ya da köşe frekansı denilen şey grafikte görülen kırılma noktasının frekans değeridir. Bu frekansdan daha küçük frekansları ve özellikle de DC değeri kayıpsız olarak çıkışa aktarıp, köşe frekansından daha büyük değerleri zayıflatmak amacıyla kullanılır. Frekans arttıkça bu zayıflatma da artar !

Şimdi geldik köşe frekansını veren formüle : f_o = R / ( 2 p L )  .  Burada

f_o : Köşe frekansı (Hz Hertz)

R  : Direnç değeri (ohm)

   L   : Bobin değeri (Henry)

p  : pi sayısı (3.1416)

Köşe frekansını hesaplamak için, önce 2 ile p ( pi = 3.1416 ) sayısını çarparız. Çıkanı bobinin Henri olarak değeri ile çarparız. Bu sonucu bir kenara not ettikten sonra, direncin değerini Ohm cinsinden alıp ve demin not ettiğimiz değere böleriz. Bu bize köşe frekansını Hertz cinsinden verir. Soruda pi sayısının değeri 3 olarak veriliyor ( küsürlü hesaptan kurtulmak için ) , f_o = 1200 / ( 2x3x20 ) = 10 Hz olarak bulunur.

Sorudaki devrenin çıkışına 100-500 µF değerinde bir kondansatör de paralel bağlanırsa besleme filtresi olarak çok daha iyi iş görür. Bu durumda hesaplar biraz değişir ama bu durumdaki hesaplar konumuzun dışında !

Doğru yanıt “d” seçeneğidir.

104. 5 KHz’lik bir giriş verilen frekans çoğaltıcıdan 60 KHz’lik bir çıkış istenirse, aşağıdaki katlardan hangisine ihtiyaç duyulur?

a) 2 frekans ikileyici ve 1 üçleyici

b) 2 frekans dörtleyici

c) 1 frekans dörtleyici ve 1 ikileyici

d) 1 frekans dörtleyici    

Çözüm : Tekrarlanan dalga şekli olan sinyale periyodik denilir. Dalga şekli sinüs ise bu sinyalde sadece bir tek frekans vardır ve bu frekans dalga şeklinin frekansı ile aynıdır. Öte yandan dalga şekli sinüs değil ama tepeleri kırpılmış bir sinüs; kare dalga veya sinüsün sadece tepelerinden oluşmuş bir dalga gibi bir şekle sahip ise, bu dalganın frekansının 1; 2; 3; 4 . . . katı olan harmonik frekansları dalga şeklinin içine gizlenmiş durumda bulunur.

Kare dalga sadece 1 ,3 , 5 , 7 , 9 . . . gibi tek sayılı harmoniklerden oluşur. Aşağıdaki 5 adet şekilde sıra ile 1 ,3 , 5 , 7 , 9 sayılı tek harmoniklerin bir kare dalgayı aşama aşama nasıl oluşturduğu gösterilmiştir.

Bu şekillerde, temel frekanstaki bir sinüse, onun tek katlarındaki frekanslarda ve uygun genlikteki sinüs dalgalarının eklenmesiyle kare dalgaya gittikçe yaklaşan bir sinyalin üretildiğini görüyoruz.

Kare dalganın üretim yönteminin bu olmadığını tahmin etmiş olmalısınız. Kare dalga genellikle mültivibratör denilen sayısal bir devre yardımıyla üretilir.

Bu açıklamalar, sinüs olmayan bir periyodik dalganın pek çok harmoniklere sahip olduğunu göstermek amacıyla verilmiştir. Kuramsal olarak 1. 2. 3 . . .  sonsuza kadar gider ama harmoniğin numarası yükseldikçe şiddeti azalır. Zaten yukarıdaki şekillerde de ilave edilen yeşil renkli her yeni harmoniğin genliğinin gitgide azalması buna tipik bir örnektir.

Bazı periyodik dalgalar, kare dalgaki gibi sadece tek sayılı harmoniklere sahip değil ama, tek numaralı harmoniklerin yanı sıra aynı zamanda çift sayılı harmoniklere de sahiptir. Periyodik bir dalga şekli ana frekans ve onun tam katları olan sonsuz adet  harmoniklerine ayrılabilir.

Periyodik ama sinüs olmayan sinyalleri, bant geçiren bir süzgeçten geçirerek içindeki bazı harmonikleri seçmek mümkün olur. Mesela kare dalgadaki 3. harmoniği seçmek için, bir tank devresinin frekansını bu dalganın 3. harmoniğine ayar eder, tank devresinin uçlarından da 3. harmonik frekansındaki sinüs sinyalini elde ederiz.  Bu sinüs şeklindeki sinyalde harmonik bulunmaz. Eğer bu sinüsten de daha yüksek harmonikleri elde etmek istersek, sinüs sinyalini bir transistör vb “C” sınıfı çalışan aktif bir  devre ile hem sinyali güçlendiririz hem de tekrar harmonik üretiriz.

İşte bu “C” sınıfı güçlendirme ve onu izleyen harmonik frekansına akort edilmiş seçici süzgeçten oluşan devreye “ frekans katlayıcı ” denir. Seçilen kat frekansı 2. harmonik ise “ikileyici” ; 3. harmonik ise “üçleyici” denir.

Bu kadar bilgiden sonra sorudaki 60 KHz.’lik  sinyalin 5 KHz.’lik sinyalden nasıl üretileceğini düşünelim. Önce 60 KHz.’lik frekans  5 KHz.’in kaç katıdır onu bulalım : 60 / 5 = 12  demek ki 12 kat elde edilecek. Periyodik bir sinyalde onikinci harmonik bukunur. Ama genliği çok az olduğu için bu yöntem ender olarak kullanılır. Onun yerine 12 sayısını oluşturacak askatlerı kullanmak derekir. 12 sayısının askatları 2 ; 3 ; 4 ve 6 olup, 2×6=12 veya 3×4=12 gibi bileşimler bulunabilir. Öte yandan genellikle 3. harmonikten daha yüksek bileşenleri kullanmak sinyal şiddeti açısından sorunlu olmaktadır. O halde 12 sayısını sadece 2 ve 3 askatlarını kullanarak oluşturabilir miyiz ? Evet 2 x 2 x 3 = 12 . Bu eşitliği elektroniğe uygularsak, iki adet çıftleyici ve bir adet te üçleyici kullanmak gereği çıkar !

Doğru yanıt “a” seçeneğidir.

105. İyonosferde, yaz aylarında en düşük iyonizasyon derecesine sahip tabaka aşağıdakilerden hangisidir?

a) F₂ tabakası      b) F₁ tabakası  

 c) E tabakası       d) D tabakası

Çözüm : iyonosferin iyon yoğunluğunu ile yükseklik arasındaki ilişki aşağıdaki grafikte görülmektedir. Bu grafikten en düşük iyonizasyon derecesi olan tabakanın “D” katmanı olduğu açıkça görülmektedir.

Doğru yanıt “d” seçeneğidir.

 Teknik  soruları cevaplamaya gelecek sayılarda devam etmek üzere hoşça kalınız.

Temel Y.  METİN      TB2CBB

 Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği , ANTRAK tarafından yayınlanan “AMATÖR TELSİZCİLİK SINAV KILAVUZU ve BAŞVURU KİTABI” içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız

96) Şekilde görülen sinyal hakkında ne söylenebilir.

a) %100 modülelidir
b) %50 modülelidir
c) Modülasyon yüzdesi çok düşüktür    
d) Aşırı modüleli sinyaldir

Çözüm : sizlere bir fikir vermesi için, modülasyon yüzdesi değişik dört dalga şeklinin resmini veriyoruz.

İlk şeklimizdeki dalganın üst tepe noktalarını birleştirir iseniz, bir sinüs eğrisinin oluştuğunu göreceksiniz. Benzer şskilde alttaki uç noktaların birleştirilmesi de bir sinüs eğrisi oluşturur. Alt ve üstte uç noktalarının birleştirilmesiyle oluşan bu şekle dalganın zarfı denir.  Düşük modülasyonda  zarfta oluşan bu iki sinüs birbirinden epeyce uzaktır. Dikkat ederseniz %50 mod. şeklinde,  zarftaki sinüsler birbirlerine yaklaşmıştır. % 100 modüleli dalgada sinüsler birbirine değmektedir. % 150 modüleli dalgada ise sinüsler birbirine geçmiştir.

% 100 modülasyondon fazlası "aşırı modülasyon" diye anılır. Taşıyıcı ve çift yan bantlı genlik modülasyonlu radyo vericilerinin yayınlarında bu durum pek istenmez.

Bu bilgilerin ışığında doğru yanıtın "d" seçeneği olduğuna dikkatinizi çekerim.

97) Yarım dalga dipol antenin fiziki uzunluğu 81 m. olduğuna göre vericinin yayın frekansı aşağıdakilerden hangisidir?

a) 672 KHz     b) 1.8 MHz    c) 879 Khz    d) 760 KHz

Çözüm : elektromanyetik dalgaların boşlukta veya Dünya atmosferi içinde frekans ile dalga boyu arasındaki ilişkiyi veren formül :

λ = 300 / f ;  veya  f = 300 / λ

λ : dalga boyu ( metre )

f  : frekans ( MHz. )

Antenin boyu 81 metre ve bu da dalga boyunun yarısı olduğuna göre tam dalga boyu 81 metrenin 2 katı olacaktır. Yani λ = 161 m. İkinci verilen formülü uygular isek, f = 300 / 161 = 1.86 MHz. çıkar. Cevaplar içinde "b" seçeneği bu sonuca uygundur. Daha kestirmeden giderek " b = 150/ f " formülünü kullanırız. Burada "b" yarım dalga dipol antenin boyunu verir.

 Meraklı okurlar aradaki farkın nereden kaynaklandığını araştırır iseler, yarım dalga dipol antenlerin boyunu veren formülün , " b = 150 / f "  değil de, "  b = k x 150 / f "  şeklinde verildiğini göreceklerdir. Burada önceki formülden tek farkın, "k" ile gösterilen ve değeri  0.95 ile 0.98 arasında seçilen bir katsayı olduğuna dikkatinizi çekelim. Yani antenin gerçek boyu, önceki formüle göre hesaplanan boydan %5 ile %2 arasında daha kısadır. Sorudaki antenin katsayısı da 0.972 olarak alınmıştır. (yani %3 daha kısa) Genelde k=0.95 olarak alınır.

98) Şekildeki dedektör devresinin E₀ çıkışında elde edilecek esas işaret üzerindeki dalgalanmayı önlemek için aşağıdaki elemanlardan hangisinin seçimi çok önemlidir?

a) C_p kapasitesi           b) C kapasitesi

c) C_s kapasitesi           d) C kapasitesi ve R direnci

Çözüm : Lp ve Ls bobinleri birbirine yakın sarılmış iki bobin olup, bir RF trafosunun primer ve sekonder sargılarıdır. Primer bobini Cp ; sekonder sargısı da Cs kondansatörüyle paralel bağlanmıştır. Bu bağlantı, her iki tarafı da akortlanmış bir ara frekans trafosu oluşturur. Dolayısıyla Cp ve Cs kapasitelerinin görevi akort olup, soruda sözedilen dalgalanmayı önlemek gibi bir işlevleri yoktur.

D₁ diyodu genlik demodülasyonu yapar. C ve R elemanları da elde edilen demodüleli işaretin üzerinden taşıyıcı kalıntılarını silmeye yarar. R ve C elemanlarının değerlerinin çarpımına " RC zaman sabiti " denir. Bu çarpım çıkıştaki ses işareti üzerindeki dalgalanmanın üzerinde çok etkilidir. Eğer bu değer çok büyük olursa (ya C veya R büyük veya her ikisi de büyük) ses işaretindeki tiz frekanslar silinir. Tersine RC çok küçük olursa da bu sefer çıkıştaki taşıyıcı işaretin izleri artar ve bu da devrenin çalışmasını bozar, hatta ıslık sesi gibi osilasyonlara sebep olabilir.

Tek başına C kapasitesinin değeri, bu işin sağliklı yapılabilmesine yetmez. Bu nedenle doğru cevap "d" seçeneğidir.

99) Şekildeki devrede köprünün üst ucu (+) ise, ilk yarım döngüde aşağıdakilerin hangisi doğrudur?

a) D₃ ve D₄ iletimdedir
b) D₂ ve D₃ iletimdedir
c) D₁ ve D₃ iletimdedir
d) Her dönüşte R_L üzerindeki akımın yönü değişir

Çözüm : Diyotların temel özelliği,  akım kaynağın "+"  ucundan çıkıp ok yönünde  anoda girerken veya ( elektronlar " – "  uçtan katoda girerken ) akımı  iletmeleridir. Ters yönde ise iletmezler( tıkama ).

Soruda köprünün üst ucu "+" olarak veriliyor. O halde D₁ tıkamada, D₂  iletimde olacaktır. Akım D₂ diyotundan yük direncinin üst ucuna girer, çünki D₄ diyotundan geçemez (tıkama). Yükün alt ucundan çıkarak D₁ ve D₃ diyotlarının birleşim noktasına giren yük akımı, trafonun alt ucuna gidebilmek için  D₃ diyotundan geçer. Bu durumda ilk yarım döngüde D₂ ve D₃ diyotları iletimdedir.

Doğru cevap "c" seçeneğidir.

100) Yukarıdaki devrede V₂ voltajının değeri nedir?

 (  I₁ = 5A,       R₂= 50 ohm,          )

a)100 V          b) 50 V c) 25 V              d) 12,5 V

Çözüm : Transfomatörlerde " V₁ / V₂ = n₁ / n₂ = I₂ / I₁ " formülleri çok kullanılır. Devrede I₁ = 5A,   R₂= 50 ohm,   n₂ / n₁ = 10  olarak verilmiş. I₂ bilinirse Ohm kanunu kullanılarak  V₂  bulunabilir. (  V₂ = R₂ x I₂ ) . Öte yandan yukarıda koyu harflerle yazılmış formüllerde n₁ / n₂ = I₂ / I₁ veriliyor. Dikkat ederseniz verilenler arasında " n₁ / n₂ " değil  de " n₂/n₁=10 " olarak verilmiş.  n₁/n₂ = 1/10 olur. (yani matematik diliyle 10 sayısının tersi.)

n₁ / n₂ = I₂ / I₁ = 1/10 = I₂ / 5 , = I₂ = 10/5 =2 A. olur.

V₂ = R₂ x I₂ = 50 Ohm x 2A. = 100 Volt olarak bulunur.

Doğru yanıt "a" seçeneğidir

Temel Y.METİN   TB2CBB

Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği , ANTRAK tarafından yayınlanan “AMATÖR TELSİZCİLİK SINAV KILAVUZU ve BAŞVURU KİTABI” içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız .

91) 1 W ve 1 M Ω 'luk bir dirençten geçirilebilecek maksimum akım aşağıdakilerden hangisidir?

a) 10^-6 A b) 10^-3 A c) 0.1 mA d) 10^-12 A

Çözüm : Bir direncin gücü ile akım arasındaki bağıntı , “ P = R x I² ” şeklinde gösterilir. Burada :P Watt cinsinden direncin gücünü ; R Ohm cinsinden direncin değerini ;I Amper cinsinden direncin akımını ifade eder. 1W = 1×10⁶ x I² ;
buradan I² = 1 / 1×10⁶ = 1×10 ^-6 ,ya da I = 1×10 ^-3 Amper = 10 ^-3 A. = 1 mA. olarak bulunur. Doğru cevap “b” seçeneğidir.

92) Şekilde bir beam anteni görülmektedir. Bu antenden gönderilen sinyaller:

a) Düşey polarizelidir b) Yatay polarizelidir
c) Eliptik polarizelidir d) Polarizeli değildir

Çözüm : Resimden anlaşıldığı kadarıyla, bu antenin elemanları düşey durumdadır. Elemanların durumu, antenden çıkan dalgaların polarizasyonu için en önemli etmendir. Yani anten elemanları düşey ise anten ve dalgalar düşey polarizasyonlu; elemanlar yatay ise antenden çıkan dalgalar yatay polarizasyonludur.Bu bilgilerin ışığında, resimdeki anten için “ düşey polarizelidir ” diyebiliriz.

Doğru cevap “a” seçeneğidir.

93) Şekildeki RLC devresinin empedansını bulunuz?

a) 32 Ω b) 33 Ω c) 13 Ω d) 14 Ω

Çözüm : Kondansatör, bobin ve dirençlerden oluşan bu tip devrelerin empedanslarının hesaplanmasında kullanılan yöntem, dirençlerden oluşan devrelerin çözümlerine benzer.Sorudaki devre seri bağlanmış üç elemandan oluşuyor. İlk işimiz direnç dışındaki iki elemanın eşdeğer reaktansını bulmaktır. Bunun için : X = X_L – X_C formülünü kullanırız. Burada,X eşdeğer reaktansı (ohm); X_L bobinin reaktansını (ohm); X_C kondansatörün reaktansını (ohm) göstermektedir.
X = X_L – X_C = 10 – 22 = -12 Ohm olarak bulunur. Bu hesaptan sonra bazı okurların “ eksi direnç olur mu yahu ? ” diyeceklerini tahmin ediyorum. Ama bir dakika durun bakalım. Size eksi dirençten söz etmedik ki ! Şimdiye kadar hep empedans ve reaktans diye bazı hayali kavramların üzerinde söz ettik. Bobin ve kondansatörlerden oluşan devrelerde eşdeğer reaktanslar eksi değerlerde olabilir. Empedansın bulunması için “ Z = √ ( R² + X² ) ” formülünü kullanacağız. Önce direncin karesini alır, ardından reaktansın karesinin hesaplar ve her iki kareyi toplayıp daha sonra da toplamın kare kökünü buluruz.
Z = √ ( R² + X² ) = √ ( 5² + (-12)² = √ ( 25 + 144 ) = √ 169 = 13 ohm olarak bulunur. Tabii (-12) nin karesinin 144 ettiğini farkettiniz. Yanınızda karekök hesabı yapabilen bir hesap makinası varsa bu işlemleri çok daha kolay yapabilirsiniz. Doğru yanıt “c” seçeneğidir.

94) Aşağıda bir amplifikatör devresi görülmektedir. R₂ ve C₁ üzerinde akıp d noktasına ulaşan akım hangisidir?

a) A transistörünün çıkış akımıdır,
b) Negatif geri besleme akımıdır
c) Yükseltecin giriş akımıdır
d) Pozitif geri besleme akımıdır

Çözüm: Doğru cevap için seçenekleri sırayla incelersek :“R2 ve C1 üzeriden akıp, d noktasına ulaşan akım”
a) A transistörünün çıkış akımı olamaz,
b) Negatiif geri besleme akımıdır çünki, R2 ile A transistörünün birleştiği nokta ile “d” noktasındaki işaretlerin fazları birbirine terstir. Bu da yapılan geri beslemenin negatif olmasına sebep olur.
c) Yükseltecin giriş akımı değildir.
d) “b” seçeneğinde sözedilen işaretlerin ters fazda olması, geri beslemenin pozitif değil negatif olması demektir.
Doğru cevap “b” seçeneğidir. Bu soru da bir önceki soru gibi ileri bir elektronik bilgisi gerektiriyor. Üstelik bu bilgiler de normal bir radyo amatörüne gerekmeyecak konuları içeriyor. Ama üzülerek görmekteyiz ki bu tür ağır sorular sınavlarda zaman zaman soruluyor ! Biz de o nedenle bu sütunlarda böyle zor ve gereksiz sorulara yer veriyoruz.

95) Aşağıdaki modülasyon çeşitlerinden hangisi genlik modülasyonu değildir?

a) Seri modülasyon
b) Transformatör modülasyonu
c) Şok modülasyonu
d) Reaktans modülasyonu

Çözüm: seçenekleri sırayla inceleyelim :
a. Seri modülasyon genlik modülasyonu yöntemidir,
b. Transformator modülasyonu bir genlik m. yöntemidir,
c. Şok modülasyonu da genlik m. yöntemidir,
d. Reaktans modülasyonu bir frekans modülasyonu yöntemidir. O halde doğru cevap “d” seçeneğidir.

Teknik soruları cevaplamaya gelecek ay da devam etmek umuduyla hoşça kalınız.

Temel Y. METİN TB2CBB

Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği , ANTRAK tarafından yayınlanan “AMATÖR TELSİZCİLİK SINAV KILAVUZU ve BAŞVURU KİTABI” içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız .

86) Aşağıdakilerden hangisi yüksek geçirgen filtredir.

Çözüm: Süzgeçlerde frekans cevabını belirleyen, çıkışa paralel elemanın cinsi veya böyle bir eleman yoksa, hayal ettiğiniz böyle bir elemana benzer şekilde saşe çizgisine dik olarak inen diğer elemanlardır. Eğer sözkonusu bileşen bir kondansatörse ve ona paralel bir bobin bağlı değilse bu devre alçak geçiren bir süzgeç olabilir. Ters olarak da bu eleman bir bobin ise (paralel kondansatör olmaksızın) devre yüksek geçiren süzgeç olabilir. Olabilir diyorum çünki bu kriter önemli olmakla beraber tek başına yeterli değildir. Şimdi sıra ile tüm seçenekleri inceleyelim : İlk seçenekte çıkışa paralel bir eleman yok, ama devrenin ortasında saşe çizgisine dik olarak bağlanan bir kondansatör var ve bu eleman girişe bir direnç ile bağlanmış… Bu devre RC alçak geçiren süzgeç tir.İkinci seçenekte çıkışa paralel bir bobin tek başına bulunuyor ve bileşen girişe bir kondansatör ile bağlanmış. Bu devre LC yüksek geçiren süzgeç olarak kabul edilir.Üçüncü seçenekte çıkışa paralel bir kondansatör yer alıyor. Ayrıca bu eleman girişe bir LC tank devresi ile bağlanmış. Bu nedenle alçak frekansları geçiren yanı sıra da tank devresinin rezonans frekansını da epeyce zayıflatan bir devredir. Bu tip devreler LC alçak geçiren ve bant durduran süzgeç diye anılır. Son seçenek RC alçak geçiren süzgeç için iyi bir örnektir.Sonuçta, doğru cevap “b” seçeneğidir.

87) 10 F lık iki kondansatör 10V, 1 kHz lik bir besleme kaynağına paralel bağlanmıştır. Akım ve gerilim arasındaki faz farkı ne kadardır.

a) 0 derece c) 60 derece
b) 45 derece d) 90 derece

Çözüm: Bir kondansatörden geçen akım, geriliminden 90 derece farklıdır. Soruda kaynağa paralel bağlı iki kondansatörden başka elemandan söz edilmediğine göre, verilen gerilim ; frekans ve eleman değerlerinin cevap için yararı bulunmamaktadır.Doğru yanıt “d” seçeneğidir.

88) Aşağıdakilerden hangi filtre HF vericinin çıkışındaki harmonikleri minimuma indirir.

Çözüm: Bir radyo amatörü frekans cevabına bakarak filtreler için yorum yapabilmelidir. Sorumuz bu konuda iyi bir örnektir. Sorulan süzgeçleri tek tek inceleyelim:İlk süzgecimiz, yaklaşık 30 MHz.’den büyük frekanslarda zayıflatma yapmayan, buna karşın 30 MHz. civarındaki köşe frekansı ’ ndan (corner frequency) daha düşük sinyalleri, frekans azaldıkça daha fazla zayıflatan bir frekans cevabına sahiptir. Bu ise HF vericinin ana frekansının antene zayıflatılarak aktarılması, harmoniklerin ise ana taşıyıcı sinyalden çok daha az zayıflamasına hatta hiç zayıflatılmamasına neden olur. Bu tip süzgeç yüksek geçiren süzgeç (high pass filter) adıyla anılır.İkinci süzgecimizin de köşe frekansı ise gene 30 MHz. civarında olmakla birlikte, frekans cevabı ilk incelediğimiz filtrenin tam tersidir. Yani köşe frekansından düşük sinyalleri zayıflatmadan geçirmesine karşın, daha yüksek frekansları gitgide daha çok zayıflatmaktadır. Bu davranış vericinin harmoniklerini çok azaltır. Bu tip filtreler alçak geçiren süzgeç diye anılır. (low pass filter)Üçüncü seçenekte verilen süzgecin köşe frekansı 30 MHz.’den daha yüksektir ve yüksek geçiren tiptedir. Bunun da işimize yaramadığı açıktır.Son seçenekteki süzgeç kademeli bir alçak zayılatma karakteristiğine ve 30 MHz. den yüksek frekanslar için iyi bir geçirme bandına sahiptir. Bu da yüksek geçiren bir süzgeçtir ve HF bandındaki bir vericinin harmoniklerini geçirip, ana taşıyıcıyı zayıflatmaktadır.Böylece doğru cevap “b” seçeneği olur.

89) Aşağıdaki devrelerden hangisi bir mikrofon devresinde bant genişliğini minimum yapmak için kullanılan bir alçak geçirgen filtredir.

Çözüm:

90) Periyodu 50 s olan frekans nedir.

a) 2 kHz b) 20 kHz c) 200 kHz d) 2 MHz

Çözüm: Periyot ile frekans arasındaki ilişkiyi veren formül :f ( Hz ) = 1 / T ( Sn ) şeklindedir. Ters olarak T sorulduğunda daT ( Sn ) = 1 / f ( Hz ) kullanılır. Bu formüllerde “f ” Hz cinsinden frekansı, “T” Sn cinsinden periyodu gösterir.f = 1 / T = 1 / ( 0.000050 Sn ) = 20000 Hz = 20 KHz bulunur.Doğru yanıt “b” seçeneğidir.

Teknik soruları cevaplamaya gelecek sayılarda da devam etmek üzere, hoşça kalınız.

Temel Y. METİN TB2CBB

Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği , ANTRAK tarafından yayınlanan “AMATÖR TELSİZCİLİK SINAV KILAVUZU ve BAŞVURU KİTABI” içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız.

81) Bazen transistörlerin bacağına küçük ferit yüzükler takılır, bunun amacı;

a) Transistör bacağını ekranlamak.
b) Transistör ile baskı devre arasında mesafe bırakmak.
c) Parazitik osilasyonları önlemek.
d) 50 ohm'a ayarlamaktır.

Çözüm : Doğru cevabı bulmak için seçenekleri sırayla incelediğimizde, ilk cevabımız yanlıştır. Elektronikte ekranlama iletken bir levha ya da tel örgüler ile yapılır. Buna karşın ferit yüzük iletken değildir. İkinci cevap da yanlıştır, baskılı devre ile transistör arasında bir aralık bırakmak için ferit yüzükten çok daha ucuz plastik yüzükler kullanılır.Üçüncü cevap doğrudur, transistörün bacağından geçen yüksek frekanslı ve yüksek şiddetteki akımlar aktıkları bacak çevresinde güçlü bir RF manyetik alanı oluşturur . ( 100 mA ve daha yüksek RF akımlar) Bu alan transistör veya diğer duyarlı devre bileşenlerine etki ederek, istenmeyen osilasyonlara neden olabilir. Bunu önlemek için ferit yüzükler takılır. Bu yüzükler, manyetik özellikleri ile bu zaralı RF manyetik alanı kendi içlerinde hapsederek dışarı çıkmasını önlerler.Son seçeneğin hiçbir bilimsel tarafı yoktur !Doğru cevap “c” seçeneğidir.

82) Bir transformatörün primer sargısı, sekonderinkinin beş katıdır. Primer sargılarına 250 V verilirse sekonderden kaç volt çıkar.

a) 10V c) 50V
b) 25V d) 1250V

Çözüm : Bir transformatörün primer sargı sayısının sekonderinkine bölümü , primer voltajının sekonder voltajına bölümüne eşittir. Matematiksel olarak şu formül verilir :
N_P / N_S = V_P / V_S ;
burada
N_P : primer sargı sayısını
N_S : sekonder sargı sayısını
V_P : primer voltajını
V_S : sekonder voltajını göstermektedir.
Soruda ( N_P / N_S ) değeri 5 olarak veriliyor. Ayrıca V_P de 250 volt olarak verilmiş . O halde
5 = 250 / V_S formülünden 5 x V_S = 250 , ya da V_S = 250 / 5 = 50 volt bulunur. Doğru cevap “c” seçeneğidir.

83) 12,5 V luk bir besleme kaynağı, çıkış gücü 90 Watt olan bir güç amplifikatörüne bağlanmıştır. Besleme kaynağından 16 A çekilmektedir. Bu amlifikatörün verimi nedir.

a) %45 c) %100
b) %55 d) %222

Çözüm : Bir cihazın verimini hesaplayabilmek için öncelikle harcanan güç ile faydalı gücün değerini bulmamız ve sonra da faydalı gücü harcanan güce bölmemiz gerekir. Harcanan güç besleme kaynağından çekilen akım ile besleme voltajının çarpımına eşittir.
P ( Harcanan ) = I x V = 16 A. X 12.5 V. = 200 W.
Verim = 90 W. / 200 W. = 0.45 = %45

84) Aşağıdaki devrenin A ve B uçları arasındaki toplam endüktans nedir.

a) 1.33 H c) 3.5 H
b) 3 H d) 6 H

Çözüm : Devrede paralel bağlı iki bobin ve onlara seri bağlanmış bir başka bobin görülüyor. Paralel bağlı bobinlerde eşdeğer bobinin değerinin hesaplamak için :
1 / L _eş = ( 1 / L₁ + 1 / L₂ + 1 / L₃ + . . . ) veya
L _eş = 1 / ( 1 / L₁ + 1 / L₂ + 1 / L₃ + . . . ) formülleri kullanılır. Bu formüller iki ya da daha fazla bobinin paralel bağlanma durumunda kullanılır. Elimizde paralel bağlı iki bobin olduğu için
L _eş = 1 / ( 1 / L₁ + 1 / L₂ ) = 1 / ( 1 / 2 + 1 / 2 ) = 1 / 1 = 1 H
değeri hesaplanır.Öte yandan bu eşdeğer bobine 2 H. değerinde bir bobinin seri bağlandığını görüyoruz. Seri bağlı bobinlerde eşdeğer bobin değerinin bulmak için toplamını buluruz. Matematik diliyle
L _eş = ( L₁ + L₂ + L₃ + . . . ) formülünü kullanırız.
L_AB = ( L₁ + L₂ ) = 2 + 1 = 3 H. değeri bulunur. Doğru cevap “b” seçeneğidir.

85) Üç farklı değerde kondansatör paralel bağlandığında toplam kapasite ne olur.

a) En yüksek değerli kapasiteden daha büyük.
b) Üçünün aritmetiksel ortalaması.
c) En düşük değerli kapasiteden daha küçük.
d) En yüksek ve düşük kapasiteli kondansatörler arasında herhangi bir değer.

Çözüm : İki veya daha fazla kondansatörün paralel bağlandığında eşdeğer kapasitenin hesabı için tüm kapasitelerin değerlerini toplarız. Bunun formülünü verelim :
C_T = ( C₁ + C₂ + C₃ + . . . ) Ana bilgi olarak bu formülün ışığında seçenekleri birer birer inceleyelim :İlk seçenekteki cevap doğrudur, çünki bir toplamın değeri toplamı oluşturan bileşenlerin hepsinden büyüktür. Dolayısıyla en yüksek değerli bileşenden de büyük olur.İkinci seçenek, formülümüzle uyuşmuyor, dolayısıyla yanlıştır.Üçüncü seçenek de formül ile çelişiyor, o da yanlıştır.Son seçenek de yanlıştır.Doğru cevap “a” seçeneğidir.

Teknik soruları cevaplamaya gelecek ay da devam etmek üzere hoşça kalınız.

Temel Y. METİN TB2CBB

Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği , ANTRAK tarafından yayınlanan “Amatör Telsizcilik Sınav Kılavuzu ve Başvuru Kitabı” içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız.

76) 1mH lik bir bobin, 1uF lık bir kondansatör ile paralel bağlanmıştır. Devrenin rezonans frekansı nedir ?

a) 0.5033 kHz c) 0.5033 MHz
b) 5.033 kHz d) 5.033 MHz

Çözüm : Bir kondansatör ile bir bobin, rezonans devresi oluşturmak için çok sık kullanılır. Bu iki bileşen ya paralel bağlanır veya seri bağlanır. Paralel bağlı bir bobin ve bir kondansatörden oluşan rezonans devresine elektronikte “tank devresi” denilir ; seri rezonans devresinin özel bir adı olduğunu ben bilmiyorum.Bu girişten sonra şunu söylemek gerekir “seri veya paralel rezonans devrelerinin rezonans frekansının hesabı için kulanılan formül :

f = 1 / ( 2 x π x √ L C ) şeklinde ifade edilir ” Burada :

f Hertz (Hz) cinsinden frekansı,
π pi sayısını (3.1416) ,
L Henry (H) cinsinden bobin değerini,
C Farad (F) cinsinden kondansatör değerini,
√ bobin ve kondansatör değerlerinin çarpımının kare kökünü göstermektedir.

Sorudaki değerler ile hesap yaptığımızda :

L = 1×10^–3 Henry ; C = 1X10^–6 Farad
LC = 1×10^–9 = 10×10^–10
√ L C = 3.1623 x 10^–5
2 x π x √ L C = 2 x 3.1416 x 3.1623 x 10^–5 = 19.869 x 10^–5
f = 1 / ( 2 x π x √ L C ) = 5033 Hz = 5.033 KHz olarak bulunur.

Doğru cevap b seçeneğidir.

77) Direnç renkleri sırasıyla Sarı, Turuncu, Kahverengi, Altın olan bir direncin değeri hangi sınırlar içindedir?

a) 425-435 ohm c) 4085-4515 ohm
b) 387-473 ohm d) 408,5-451,5 ohm

Çözüm : bu soruyu cevaplamak için dirençlerin renk tablosunu ezbere bilmek gerekir. Ezberlemeyen okurlar için bu tabloyu aşağıda veriyoruz.

Tablodan ilk renk olarak sarı renk karşılığı olan 4 rakamını ve ikinci sayı olarak da 3 (turuncu) , çarpan olarak da 10 (kahverengi) bulunur. İlk iki rakam yanyana yazılınca 43 sayısı bulunur. Bu sayı çarpan ile çarpılınca 430 ohm değerinde bir direnci anlarız.

Dirençler belli bir tolerans içinde üretilir ve değerleri ona göre kodlanır. Elimizdeki direncin toleransı için de tabloya dördüncü renk için bakarız. Altın rengine karşılık gelen tolerans %5 tir. Yani direncimiz 430 değerinin %5 eksiği olan bir değer ile %5 fazlası olan bir değer arasında herhangi bir değere sahip olacak demektir. Kolaylık olması için bir formül verelim:

R . ( 1 – t ) ≤ R_x ≤  R . ( 1 + t ) burada :

R direncin anma değerini (sorudaki değer 430 ohm)
t toleransı (soruda %5 veya matematik diliyle 5/100 = 0.05)
R_x direncin gerçek değerini göstermektedir.

Değerleri yerine koyarsak:

430 x (1-0.05) ≤ R_x ≤ 430 x (1+0.05)

430 x (0.95) ≤ R_x ≤ 430 x (1.05)

408.5 ohm ≤ R_x ≤ 451.5 ohm olarak bulunur.

Doğru cevap “d” seçeneğidir.

78) 3.73 MHz deki bir vericinin ikinci harmoniği nedir?

a) 1.865 MHz c) 10.19 MHz
b) 7.46 MHz d) Hiçbiri

Çözüm : vericilerin çıkışlarında periyodik dalga şekli olan bir sinyal bulunur. Bu sinyalin ikinci harmoniği demek, o sinyalin temel frekansının iki katı olan sinyal demektir. Bu nedenle temel frekansı 3.73 MHz olan bir vericinin ikinci harmoniğini hesaplamak için temel frekansın iki katını bulmamız gerekir : 3.73 MHz. x 2 = 7.46 MHz.
Doğru cevap “b” seçeneğidir

79) SSB yayınlarını elde etmek için kullanılan metod hangisidir?

a) Faz kaydırma metodu.
b) Filtre metodu.
c) a ve b nin ikiside kullanılır.
d) a ve b nin hiçbiri kullanılmaz.

Çözüm : tek yan bant anlamına gelen “SSB” işaretini üretmek için genellikle filtre metodu kullanılır. Kuramsal olarak “Hilbert” dönüşümü ile ifade edilen faz kaydırma metodu da yaygın olmamakla beraber kullanılmaktadır.
Doğru cevap “c” seçeneğidir.

80) 300 ohm luk bir verici antenini alıcımıza 75 ohm değerinde bir koaksiyel kablo ile bağlamak istiyoruz. Araya konulması gereken balun’un sargı oranı ne olmalıdır?

a) 1:1 c) 1:4
b) 1:2 d) 1:16

Çözüm : Balun, sargılardan oluşan ve RF’de çalışan bir çeşit transformatördür. Transformatörlerin sargı oranları, o sargılardaki voltaj değerleri ile orantılıdır. Ama iş empedansa gelince durum değişir ve trensformatör empedansları sargı oranının karesi ile değiştirir. Yani ½ sargı oranı olan bir balun voltajı da ½ oranında değiştirir ama empedansı ½ x ½ = ¼ oranında değiştirir.
Tesadüfen sorudaki empedans oranı da 75 / 300 = 1 / 4 olduğu için,1 / 2 oranında bir baluna ihtiyacımız var.

Doğru cevap “b” seçeneğidir.

Teknik soruları cevaplamağa gelecek ay da devam etmek üzere hoşça kalınız.

Temel Y. METİN TB2CBB

Radyo amatörlüğü lisans sınavında sorulan elektronik ile ilgili soruların pek çok örneği , ANTRAK tarafından yayınlanan "AMATÖR TELSİZCİLİK SINAV KILAVUZU ve BAŞVURU KİTABI" içinde yıllardır yer almaktadır. Bu kitapta soruların cevap anahtarları da vardır. Burada ise bu teknik sorulardan bir bölümünün çözümlerini bulacaksınız .

71) 0.1 volt , mV cinsinden nasıl gösterilir.

a) 1 mV         b) 10 mV       c) 100 mV        d) 1000 mV

Çözüm :   volt cinsinden verilen bir gerilimi mV. ( milivolt ) cinsinden ifade edebilmek için 1000 ile çarparız. Örneğin 2 volt değerindeki bir gerilim milivolt cinsinden 2 x 1000 = 2000 mV. şeklinde ifade edilebilir. Benzer şekilde 0.1 V. da 0.1 x 1000 = 100 mV. değerine sahiptir. Cevapların içinde "c" seçeneği doğrudur.

Ters bir çevirim yani milivolt (mV.) ile ifade edilen bir değeri volt (V.) şeklinde ifade edebilmek için de 1000 değerine böleriz. Örneğin 5000 mV. gerilim 5000 / 1000 = 5 V. şeklinde de ifade edilebilir.

72) Şekilde görülen sembol;

Çözüm :   Bu sorunun cevabı PNP transistörüdür. Doğru cevap da "a" seçeneğidir.

Seçeneklerdeki malzemelerin sembolleri aşağıda gösterilmektedir.

73)  Aşağıdaki şekilde görülen devre;

       a)Güç doğrultucusudur                      b) Bir FM diskriminatörüdür

       c) Bir varaktör tunerdir                        d) A.M. dedektördür

Çözüm : doğru cevabı bulmak için her seçeneği tek tek incelemeye başladığımızda, devrenin girişinde "10.7 MHz. IF input" ifadesinden bu devrenin 10.7 megahertz frekansında ara frekans üzerinde bir işlem yaptığını anlıyoruz. Bu nedenle "güç doğrultucusu" cevabını elemiş olduk.

Devrede herhangi bir varikap veya varaktör bileşenin bulunmaması "c" seçeneğini de elemiş oluyoruz. Kullanılan frekansın 10.7 megahertz oluşu ve bu frekansın genellikle FM ara frekansı olarak kullanılması "b" seçeneğinin gözümüze daha çekici gelmesine neden olabilir. Aman dikkat ! ! !

Devreye biraz daha dikkatle bakınca bunun FM diskriminatör devrelerine değil, A.M. detektöre benzediğine dikkatinizi çekerim. Eveet bir sinyal diyotu ve çıkışına bağlı 1000 pF kondansatör… AM detektörün ta kendisi , o halde cevap "d" seçeneğidir.

74) Aşağıdaki devrede A ve B noktaları arasındaki voltaj ne kadardır.

        a) 2.2 Volt            b) 5 Volt             c) 8 Volt             d) 5.6 Volt

Çözüm : 330 ohm direnç, zener diyot, ve 10 mikrofarad (10 uF) kondansatörden oluşan devre ilkel bir voltaj regülatörüdür. Yani zener diyotun uçlarında 5.6 volt civarında bir doğru gerilim vardır.

Buraya bağlanan ve birkaç mA. kadar akım çeken hafif yükleri beslemek için kullanılabilir. Ama bu noktadan çekilen akım artarsa, zener diyotun akımı azalır ve voltajı düşer yani regülasyon bozulur.

Bu olayı önlemek ve devreden daha fazla akım çekebilmek için NPN tipinde bir transistör tampon yükselteç olarak kullanılır. Yukarıdaki bağlantı "emetör izleyici" denilen bir devredir. Bu bağlantı İngilizcede "emitter follower" veya "common collector" diye anılır. Dilimizde aynı devreye bazen "ortak kollektörlü yükselteç" denilmektedir.

Devrenin adlandırılmasını bir kenara bırakalım da özelliklerinden biraz söz edelim :

–Devrenin voltaj kazancı "bir" ( 1 ) civarındadır. Yani çıkış voltajı ya girişe eşittir ya da girişten çok az miktarda daha azdır.
–Devrenin akım kazancı transistörün akım kazancı yani "beta" civarındadır.
–Devrenin giriş empedansı epeyce yüksektir.
–Devrenin çıkış akımının hemen hepsi kollektör aracılığıyla regülesiz besleme üzerinden sağlanır. Yani bazdan, dolayısıyla zener diyottan çok çok az akım çeker. Zaten tampon yükselteçten beklenen fonksiyon da budur.

Giriş voltajı 5.6 volt olan tampon devremizin çıkış voltajı da yaklaşık giriş voltajına eşit ya da ondan daha az olacak demektir. Ama durun ve hemen "5.6 Volt" cevabını seçmeyin. Çünkü tampon yükseltecin özelliklerini yukarıda sıralarken, giriş ve çıkış arasındaki DC ilişkinin nasıl olduğunu henüz anlatmadık. Silisyumdan yapılmış bir NPN transistörün bazı ve emetörü arasında yaklaşık 0.6 volt kadar fark vardır. Bu voltaj farkı baz ile emetör uçları arasındaki diyotun voltajıdır. Bizim devremizde emetör gerilimi bazdan yaklaşık olarak 0.6 volt kadar daha az olacaktır. Eh bu kadar açıklamadan sonra hemen herkes çıkış voltajının 5.6 – 0.6 = 5.0 Volt olduğunu kafadan hesaplamıştır. Evet sevgili okurlar çıkış gerilimi 5 Volt olup, doğru cevap "b" seçeneğidir.

75) Bir vericinin çıkış empedansı 50 ohmdur. En yüksek güç aktarımı için yük direnci ne olmalıdır.

        a) 50 ohm          b) 75 ohm              c) 100 ohm             d) 150 ohm

Çözüm : elektrik ve elektronikte en yüksek güç aktarımı sık sık karşılaştığımız bir konudur. Bu nedenle konunun temel ilkesinin akıldan çıkmayacak şekilde bilinmesinde fayda vardır. Zaten bilinmesi gereken ana ilke zor bir şey değil:

–bir sinyal kaynağından en yüksek gücü alabilmemiz için bağlamamız gereken yük empedansı, kaynağın empedansına eşit olmalıdır. (işin aslını aramak gerkirse bu konunun yüksek matematik gerektiren bazı tarafları da var, ama şu anda kafa karıştırmaya gerek yok …) Bilmemiz gerken ana kavram kaynağın empedansı ile yükün empedansı eşit olmalıdır. Ya da kaynağın çıkış direnci ve yükün direnci eşit olacak. İşte hepsi bu kadar basit .

Sorunun cevabına eğilecek olursak, vericinin çıkışı 50 Ohm olduğuna göre yükün empedansı da buna eşit olmalıdır. Doğru cevap "a" seçeneğidir.

Teknik soruları cevaplamaya devam etmek üzere hoşça kalınız.

Temel Y. METİN TB2CBB